[10000印刷√] ƒX[ƒp[ƒNƒ‹ƒbƒNƒX 988113-Prove that b(x n p) = b(n-x n 1-p)

 P a yme n t o f F i l i n g F e e (C h e ck t h e a p p ro p ri a t e b o x) ☒ N o f e e re q u i re d ☐ F e e co mp u t e d o n t a b l e b e l o w p e r E xch a n g e A ct R u l e s 1 4 a4 Convolution Solutions to Recommended Problems S41 The given input in Figure S411 can be expressed as linear combinations of xin, x 2n, X3n x, n When A and B are independent events, or in other words when the probability of "A given B" is the same as the probability of A by itself Unfortunately, if you dig a little into the definition of conditional probability (ie, what I mean when I say the probability of "A given B") you'll find that mathematically the statement P(A n B)=P(A) x P(B) is the definition of "A and B are

Splitting Of Poisson Variables Mathematics Stack Exchange

Prove that b(x n p) = b(n-x n 1-p)

Prove that b(x n p) = b(n-x n 1-p)-N { b N XCCOFC ́A } C N y ނ̐ڑ p r ɓK L m P u ł BOFC f ނ g p ̗򉻂 ጸ B v G W j A ̎g p ɑς 鍂 i A ̃P u ł B p r ɍ 킹 7 ނ̒ p ӂ Ă ܂ BPA ̌ X ^ W I A3pin DMX P u ȂǂɍœK ł BDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US

Amazon Com Panda Ultra Wifi B G N 150mbps Wireless N 2 4ghz Usb Adapter Windows Xp Vista 7 Mac Os X Ubuntu 12 04 Tls Fedora 17 And Puppy 5 3 3 Compatible Computers Accessories

N b N x W p I t B V T C g O v Ŏg p H ނ͔̍ y сA ~ j ` A J E t @ x ̎ s Ă ܂ B n V R ō͔ S S ̐H ނ͊e X g ł オ 蒸 ܂ B1349 Let x;y 2R, where R is a commutative ring with prime characteristic p a Show that (xy)p = xp yp b Show that, for all positive integers n, (xy)pn = xpn ypn c Find elements x and y in a ring of characteristic 4 such that (xy)4 = x4 y4 1View Answer Answer c Explanation We know that, the ztransform of a signal x (n) is X (z)= \sum_ {n=\infty}^ {\infty} x (n)z^ {n} Given x (n)=δ (nk)=1 at n=k => X (z)=z k From the above equation, X (z) is defined at all values of z except at z=0 for k>0 So ROC is defined as Entire zplane, except at z=0

V ł Ȃ₩ ȃt @ C o ( p v { h) f ނ g p L p e BF V Y i { k ̐j t Ƃ @ ۂ̒ i ȃp v f ނ 5 w ɏd ˈ k p i ɑ厖 ȋ x ϋv ܂ Ȃ₩ d ƒe ͐ 킹 f ނȂ̂Ť ܂ꂽ 芄 ɂ ő ɐ ƍl ܂ \\ ʂ̝ H ʼn ɂ ̂ ł ⤏ ɍœK ł L p e B ̃X g b N { b N X @ t ^ t/S T C Y DCM I C ł͔̔ Ă ܂ B ̑ ̃L b ` L p e B ̃X g b N { b N X @ t ^ t/S T C YB X ֗p ̃X ^ v X ^ v Ȃ őf A L C ɂ ܂ 4 ~60mm p V ` n ^ i y B zXKS ̂ ߁A 邢 ́A p @ ̌ ؁A Ă܂ A B X ֗p ̃X ^ v X ^ v Ȃ őf A L C ɂ ܂ 4 ~60mm p V ` n ^ i y B zXKS Ɠ ̃Z N V ̐l C ̍ i ⃂ m l ́A ʂ A C e ␻ i L O \ ⃊ X g ɉ āA i ԗ T C g A P ^ C X g b v ɍڂ Ă 鏤 i ␻ i r Ă BProof of x n algebraicaly Given (ab) n = (n, 0) a n b 0 (n, 1) a (n1) b 1 (n, 2) a (n2) b 2 (n, n) a 0 b n Here (n,k) is the binary coefficient = n

Fermat's equation, x n y n = z n with positive integer solutions, is an example of a Diophantine equation, named for the 3rdcentury Alexandrian mathematician, Diophantus, who studied them and developed methods for the solution of some kinds of Diophantine equationsA typical Diophantine problem is to find two integers x and y such that their sum, and the sum of their squares, equalFor X, where X and C are M × N real matrices, A is an M × M real matrix, and B is an N × N real matrix A familiar example occurs in the Lyapunov theory of stability 1, 2, 3 with B = AT Is also arises in the theory of structures 4 Using the notation P ×Q to denote the Kronecker product (PijQ) (see 5) in which each30 Find the values of p for which the series X∞ n=1 lnn np is convergent Answer When p ≤ 0 the terms in the series do not go to zero, so the series will diverge When p > 0, the function f(x) = lnx xp and the series satisfy the hypotheses of the Integral Test, so the series will converge if and only if Z ∞ 1 f(x)dx = Z ∞ 1 lnx xp dx

At The Point P A A On The Graph Of Y X N N Epsilon N In The First Quadrant A Normal Is Drawn The Normal Intersects The Y Axis

4 2b Finding Binomial Probabilities Binomial Probability Formula Ncxpᵡqᶮ ᵡ N Math Prb Ncr X P X Q N X N Trials X Successes P Probability Of Ppt Download

Description x = B/A solves the system of linear equations x*A = B for x The matrices A and B must contain the same number of columns MATLAB ® displays a warning message if A is badly scaled or nearly singular, but performs the calculation regardless If AUploaded By gaganow Pages 546 This preview shows page 339 343 out of 546 pages@ @ @ @ @ @ Ђъ } 邽 ߓ Ђ X p N b N X g p ܂ B @ 15 N9 v H @ 15 N11 B e

Taylor Series Wikipedia

Ols Theoretical Review Assumption 1 Linearity Y X Or Y X Where X Kx1 Assumption 2 Exogeneity E X 0 E X Lim Ppt Download

Solution This is a proof by induction on n The base case when n= 1 is clear, as 1 0 = 1 = 1 1 p 3 is irrational) Prove that every in nite set has a countably in nite subset Solution Let X be an in nite set Since X is nonempty, there exists some xN bn= k=0 n k an kbk where n k =!Theorem 8 Algebra of Power Series Let f x n a n x n and g x n b n x n from MATH at University of Guelph

If P B 3 13 And N S 52 Then N B Brainly In

Clarification For Proof Of Mathbb Q Being Dense In Mathbb R Rudin S Pma Mathematics Stack Exchange

P ancn converges Then we note that X ancn ˘ X anbn ¡ X anb ˘) X anbn ˘ X ancn ¯b X an, and the right side of the equation consists of two convergent sequences, so P anbn converges b0 •b Then bn must be increasing, so let cn ˘b¡bn, which is monotonic decreasing, so it satisfies (b) Once again, lim n!1 cn ˘0, so it satisfies (cStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeŔ탊 N I N W S O O O ꊇ o ^ \ t g y N } b N X z N W 𗘗p SEO ΍ Ɍ Ȃ 탊 N ꊇ B I N ł ȒP N W ꊇ o ^ \ t g ̊ z A ɁA ̔ ̌ ؁A āA Ŕ탊 N I N W S O O O ꊇ o ^ \ t g y N } b N X z N W 𗘗p SEO ΍ Ɍ Ȃ 탊 N ꊇ B I N ł ȒP N W ꊇ o ^ \ t g Ƌ ʂ̎g p @ ̂ ̏ 񋳍ނ ` F b N ɂ́A ̏ 񋳍ރ L O \ ̑ ɁA ̃z y W APC 傫 @ ňē Ă

If X To B N 10 P And E X 5 Then P And Var X

St2334 Studocu

Example 715 67 Consider the equation x n 1 x n b n x n 1 n 1 2 3 where b n n 1 Example 715 67 consider the equation x n 1 x n b n x School IIT Kanpur;For x = 1, the series is a divergent pseries, and for x = −1, the series is an alternating series, and since √1 n is decreasing and converges to zero, the series converges The interval of convergence is therefore −1,1) 5 XKvox i n { b n x j ́a i d p u e r l n ^ ł y p u progress1 p u ccofc pcofc ofc4e6s ofc4s6 r l n ^ kp3fx kp3mx kp3fxb kp3mxb kp3fdl kp3mdl kp3fdlb kp3mdlb kp2c kp3c kl

Amazon Com Panda Ultra Wifi B G N 150mbps Wireless N 2 4ghz Usb Adapter Windows Xp Vista 7 Mac Os X Ubuntu 12 04 Tls Fedora 17 And Puppy 5 3 3 Compatible Computers Accessories

1 Vytah

Course Title IS MISC;X1 n=1 2nsin 1 n Answer Notice that the terms of this series are not going to zero lim n!1 2nsin 1 n = lim x!1 2xsin 1 x = lim x!1 sin 1 x 1 2x = lim x!1 cos 1 x 2 2 2 (2x)2 = lim x!1 12cos x x2 4x2 2 = lim x!1 4cos 1 x = 4 where I went from the second to the third lines using L'H^opital's Rule Since the limit of the terms is equal toWhere a n represents the coefficient of the nth term and c is a constant Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functionsIn fact, Borel's theorem implies that every power series is the Taylor series of some smooth function In many situations c (the center of the series) is equal to zero, for instance when considering

Solved Let N Be Geometric With Parameter 0 P 1 That Chegg Com

Starter The Probability That A Particular Page In A Maths Book Has A Misprint Is 0 2 Find The Probability That Of 12 Pages In The Book 4 Of Them Have Ppt Video Online Download

Antiques Truffle @ A e B N X @ g t @ s s 掭 P J m O 66 @ J T u Z1 e @ @ Tel/Fax @ wwwantiquestrufflecomX ` } N b N X o C p (M) S F165mm n ̂̒ F68mm u h ށF 440C n h ށF R R {@ans13 P ̂S Ԗڂ̃` F b N { b N X ̓ ł D i b JavaScript ł͔z ̔ԍ ͂O n ܂ ܂ D j @n2t() @ ́@number to true @ 𗪂 ł D z v f 1 Ȃ true Ԃ C0 Ȃ false Ԃ ܂ D

How To Prove The Approximation Properties Of Taylor Polynomials Mathematics Stack Exchange

Answered P N Given Below Is The Price P In Bartleby

Ȃ₩ Œ y ʤ t y X ^ ѡ v ł Ȃ₩ ȃt @ C o ( p v { h) f ނ g p L p e BF V Y i { k ̐j t Ƃ @ ۂ̒ i ȃp v f ނ 5 w ɏd ˈ k p i ɑ厖 ȋ x ϋv ܂ Ȃ₩ d ƒe ͐ 킹 f ނȂ̂Ť ܂ꂽ 芄 ɂ ő ɐ ƍl ܂ \\ ʂ̝ H ʼn ɂ ̂ ł ސ } K W b N ϔ ɂ g ܂ L p e B ̃X g b N { b N X @ n M O ^ C v DCM I C ł͔̔ Ă ܂ B L p e B ̃X g b N { b N X @ n M O ^ C v DCM I C ł͔̔ Ă ܂ BȂ₩ Œ y ʤ F X g ӂ t X g b N { b N X!X IPSiO GX p C N { b N X ^ C vE5500 ̃v ^ A R s /FAX p T C N i ́A i ł Ȃ i d ɓO Ă ܂ B u ISO 9001 E ISO E STMC E d p } N v F ؎擾 H ̐ i 𒆐S ɔ̔ Ă A IPSiO GX p C N { b N X ^ C vE5500 ́A K ̃ T C N H Ɋ  A e H ɂ āA n Z p ҂ J ɍ Ƃ S Ă ܂ B ̂悤 Ȋe H ł́A { A i i IPSiO GX p C N { b N X ^ C vE5500 ̃ T C N i H 蒼 ܂ B

A B C Be Three Sets Such That N A 2 N B 3 N C 4 If P X Denotes Power Set Of X Then Brainly In

Splitting Of Poisson Variables Mathematics Stack Exchange

1 6= 0 and so p(x) is also degree 1 Inductive Step Suppose the statement is true for all polynomials of smaller degree than n De ne g(x) = P n 1 k=0 c kx k, so f(x) = g(x)c nxn Now g(x) is a polynomial of lower degree so we can apply the induction hypothesis to it If q(x) = g(x a), q is also polynomial of the same degree as g, and we2 n 1 provided n 1 2= B (if n 1 2 B then we are done since n 1 j 2n 2) This gives us some new set C = (B nf2n2g) fn1gThat is, we have thrown out the element 2n 2 and replaced it with the element n 1 We need to check that this does not invalidate the problem Notice that this trick will be dangerous if n 1 is divided by some element of B that 2n 2 is not divided by or

Ex 3 2 22 If N P The Order Of Matrix 7x 5z Is Ex 3 2

Taylor Series Wikipedia

Answered Select All Of The Following Which Are Bartleby

If X B N P Such That 4p X 4 P X 2 And N 6 Find The Distribution Mean And Standard Deviation Sarthaks Econnect Largest Online Education Community

Solved Binomial Distribution B X N P Is Defined As Fo Chegg Com

Suppose That X Is A Binomial Random Variable With 0 And P 0 4 Approximate The Following Probabilities A P X 70 B P 70 X 90 C P X 80 Homework Help And Answers Slader

Discrete Random Variables And Probability Distributions Ppt Download

Answered The Legendre Polynomial Pn X Has A Bartleby

Binomial Theorem Wikipedia

Exploring The Performance Of Pristine And Defective Silicene And Silicene Like Xsi3 X Al B C N P Sheets As Supercapacitor Electrodes A Density Functional Theory Calculation Of Quantum Capacitance Sciencedirect

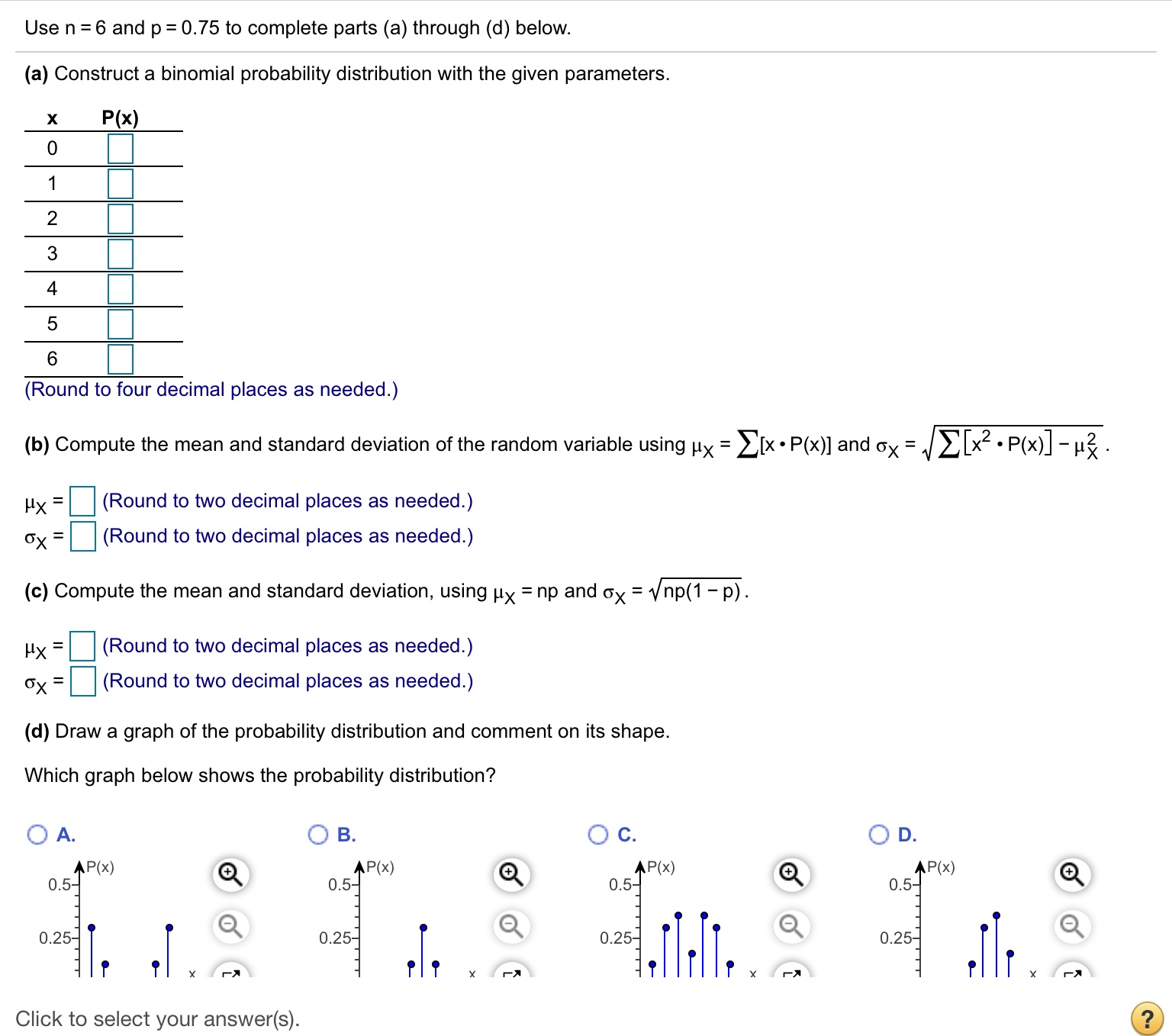
Answered Use N 6 And P 0 75 To Complete Parts Bartleby

The Binomial Distribution

Legendre Function

A If N A 6 And N Axxb 42 Then Find N B B If Some Of The

Chapter 8 Sets And Probabilities 8 1 Sets

Legendre Function

List With The Notation Used In Algorithm 2 Symbol Definition X P N Download Table

If X B N P With N 10 P 0 4 Then E X 2

Pdf 2 A Moebius Invariant Space Of Polyharmonic Functions On The Unit Ball Of R 2n

Given X Pn N And Y Pn N 1 What Can Be Concluded Gauthmath

Legendre Function

Solved A Let P X 2x2 5x 3 M X 2x 1 And H X Chegg Com

A Pressure Distribution Y P N X Of Modes 1 To 4 Obtained With A Download Scientific Diagram

Chapter 4 The Mean And Variance 4 1

Binomial Theorem For Any Index

Answers Herstein

For X B N 10 P 0 2 P X Le 8

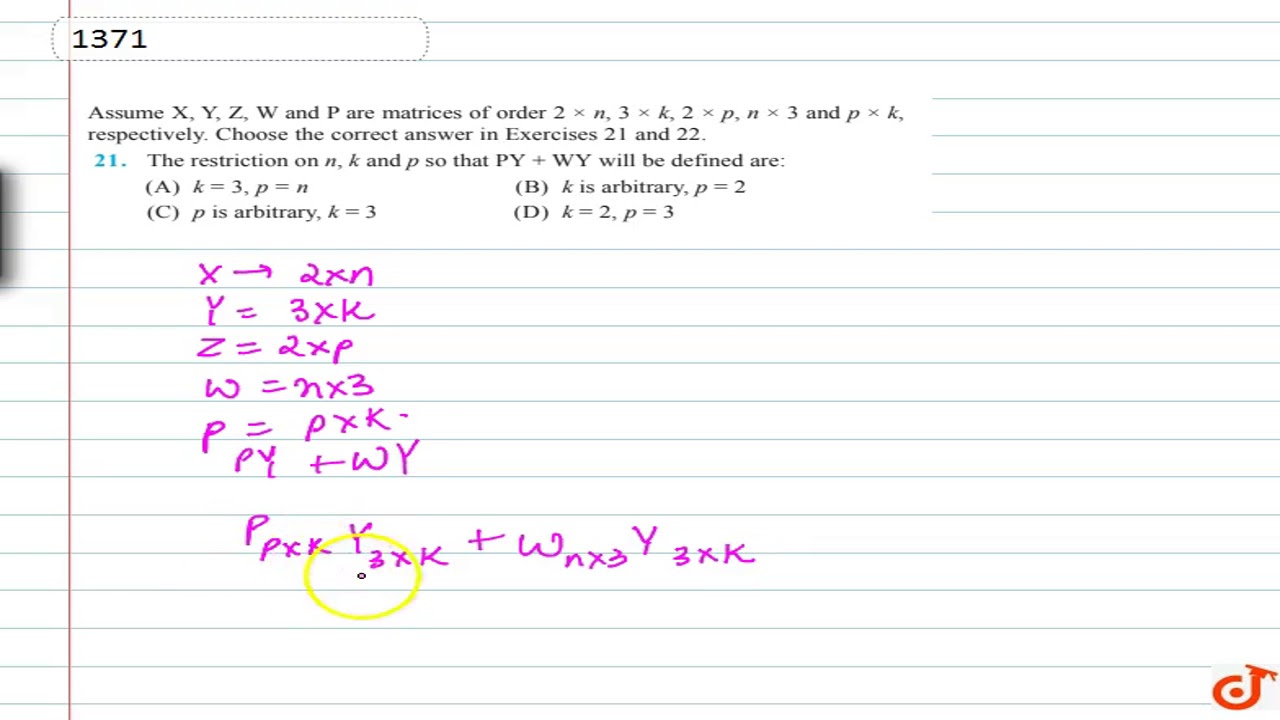
Assume X Y Z W And P Are Matrices Of Order 2 Xxn 3 Xxk 2 Xxp N Xx3 And P Xxk Youtube

Predicate Logic Answer Discrete Structures Computer Science Cse 260 Docsity

Chapter 4 Discrete Random Variables And Their Probability

Programming Languages And Compilers Cs 421 Elsa L

Find The Limiting Distribution Of Bn Frac 1 Alpha X N Cross Validated

Which Of The Following Is Are True S1 ǝx P X X Q X X P X Q X Techtud Youtube

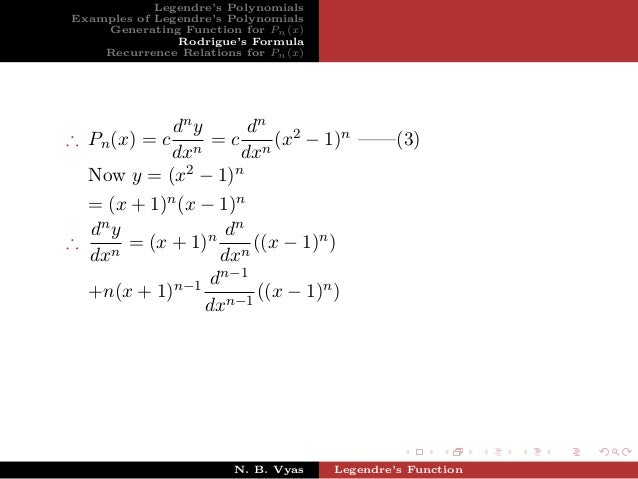
Legendre Function

7 8 Transcendency

Solved 1 Point If X Is A Binomial Random Variable Comp Chegg Com

Define A Sequence Pn Of Functions By The Formula Chegg Com

Chapter 8 Counting Principles Further Probability Topics Ppt Download

Solved Compute The Probability Of X Successes Us

Given X B N P If P 0 6 E X 6 Then The Value Of Var X I

2 Let H And K Be Subgroups Of A Group G Show That H K G If And Only If H K Or K H Pdf Free Download

Maths Hl Ib Stats Exam Binomial Distributions Franklyandjournal

Lucas Polynomial Sequence From Wolfram Mathworld

6 2 Discrete Probability Distributions Discrete Uniform Distribution

Solved The P F Of A Binomial Distribution Is F X N Chegg Com

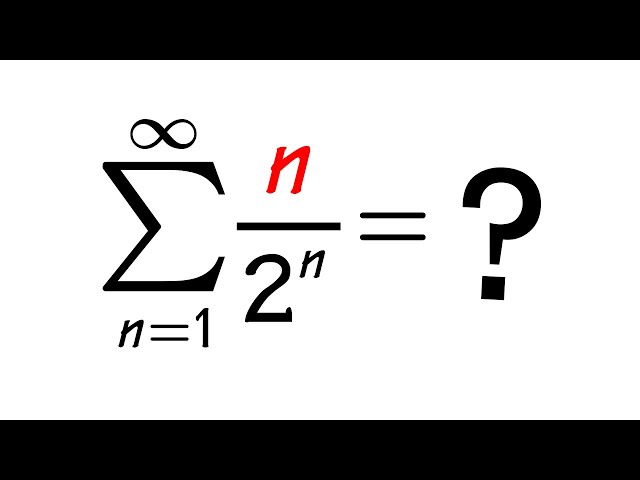
How To Find The Sum Of N 2 N Youtube

Given X Pn N And Y Pn N 1 What Can Be Concluded Gauthmath

The Distribution Of The Average Prime Divisor Of An Integer

Simplifying Polynomials In One Variable Using Quadratic Form Theory

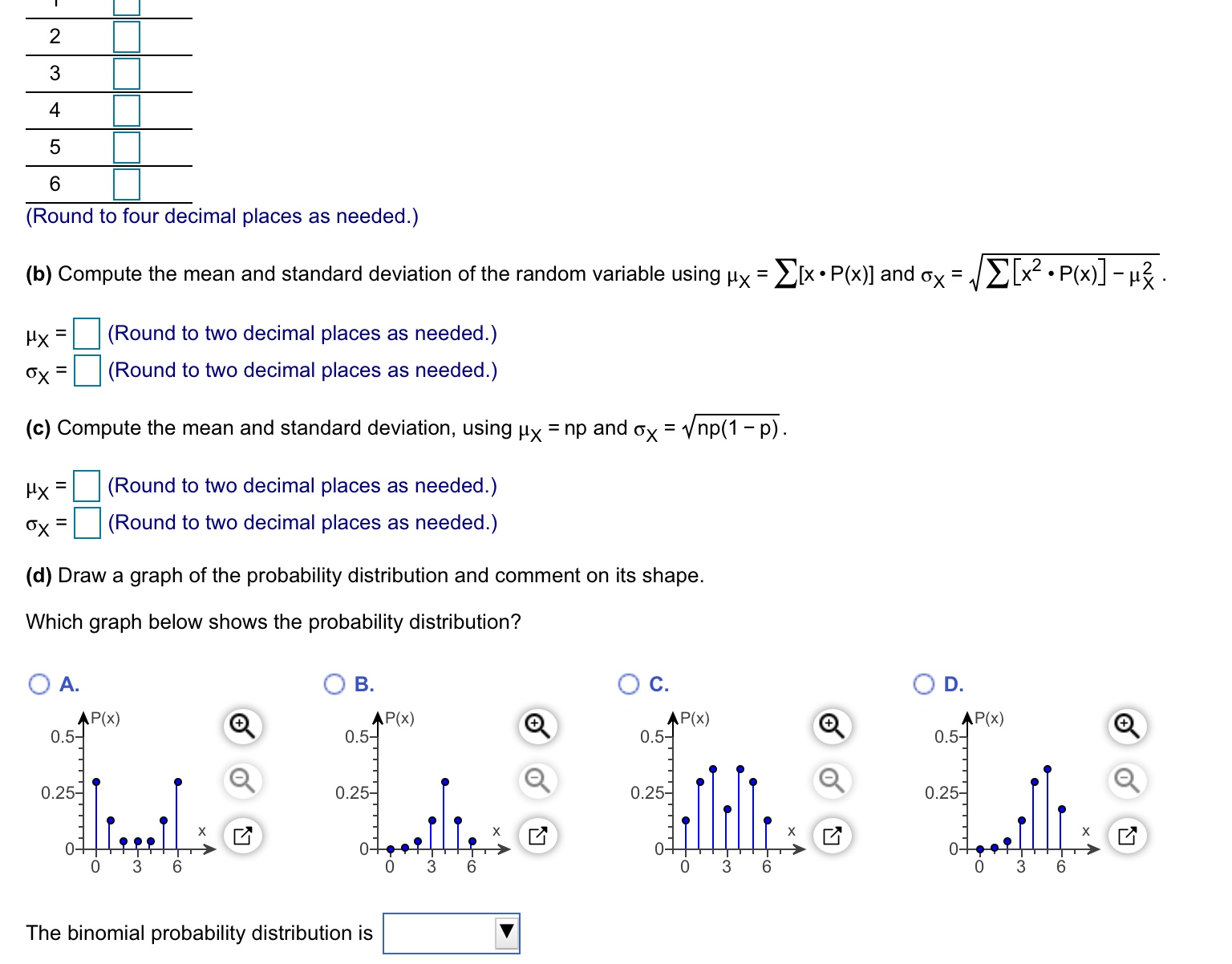
Answered Use N 6 And P 0 75 To Complete Parts Bartleby

Solved Prove Trivially That Rho Xy Sigma Infinity N Chegg Com

Continuous Hahn Polynomials Wikipedia

Solved Compute The Probability Of X Successes Us

For X B N P And E X 12 Var X 4 Then The Value Of N

Misc 12 Find Derivative Ax B N Chapter 13 Class 11

Frobenius Inequality Rank Mathematics Stack Exchange

Incoming Term: prove that b(x n p) = b(n-x n 1-p),